EXPONENTIELLE ET LOGARITHME

EXPONENTIELLE ET LOGARITHME

Pour les constructeurs des premières tables, les logarithmes étaient avant tout un outil de calcul numérique; mais leur importance n’a cessé de croître. Il suffira de feuilleter cette encyclopédie pour constater que, de nos jours, les logarithmes et les exponentielles interviennent dans tous les domaines de l’activité humaine, qu’il s’agisse de physique, de médecine, de sciences humaines... C’est le cas de tout phénomène naturel dans lequel deux mesures x et y sont telles que le taux de variation y / x de y est proportionnel à y ; la quantité y dépend alors exponentiellement de x , car on a y = ky . Mais les exponentielles s’introduisent aussi dans de nombreux autres cas; c’est ainsi que les lois de Laplace-Gauss ou de Poisson sont des techniques de base de la statistique.

En tant que fonctions nouvelles, les transcendantes élémentaires (logarithmes, exponentielles et fonctions trigonométriques) se sont introduites d’une façon naturelle au cours du XVII^e siècle, à partir de considérations cinématiques tout d’abord (étude de la cycloïde par exemple). Avec les débuts du calcul infinitésimal, ces fonctions acquièrent une grande importance théorique: découverte de leurs développements en série et rôle essentiel qu’elles jouent dans l’intégration de nombreuses équations différentielles simples. Au XVIII^e siècle, le mathématicien suisse L. Euler, par extension au champ complexe, a mis en évidence les liens étroits qui existent entre ces fonctions et a introduit les notations que l’on utilise encore aujourd’hui.

Dans ce qui suit, on construit complètement ces fonctions à partir du logarithme népérien, primitive de 1/x , en se limitant à l’aspect théorique sans aborder l’aspect pratique des calculs. Cet article est en liaison étroite avec l’article histoire du CALCUL NUMÉRIQUE.

1. Résultats préliminaires

Soit R le groupe additif des nombres réels; les nombres réels strictement positifs forment un groupe pour la multiplication que nous noterons R⁺. On se propose ici de décrire tous les homomorphismes continus de ces groupes entre eux. Ainsi, les fonctions logarithmes , les fonctions exponentielles et les fonctions puissances sont des applications continues f , g , h :

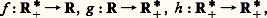qui vérifient respectivement les relations fonctionnelles:

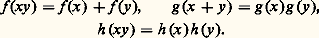Montrons pour commencer que les seuls homomorphismes continus du groupe additif R dans lui-même sont les homothéties . Soit donc:

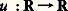une application continue telle que u (x + y ) = u (x ) + u (y ); posons u (1) = a . Pour montrer que u (x ) = ax pour tout nombre réel x , il suffit, à cause de la continuité, d’établir ce résultat pour x rationnel. Remarquons d’abord que la relation fonctionnelle entraîne:

pour tout entier positif n ; d’autre part, u (1) = u (1 + 0) = u (1) + u (0), d’où u (0) = 0. Pour les entiers négatifs, on a: 0 = u (0) = u (n + (face=F0019 漣n )) = u (n ) + u (face=F0019 漣n ), d’où:

ainsi, u (x ) = ax pour tout entier relatif. Soit enfin x = p /q un nombre rationnel; on a:

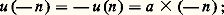
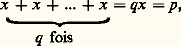d’où: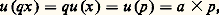

et finalement:

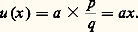Pour a = 0, on obtient l’application nulle et, pour a 0, ces homomorphismes sont des isomorphismes , c’est-à-dire qu’ils sont bijectifs.

Il est facile de voir que la continuité de u équivaut à la continuité à l’origine, ou encore au fait que u soit bornée au voisinage de zéro. On peut même démontrer que la mesurabilité de u suffit; en revanche, si l’on n’impose aucune condition, on peut montrer, en faissant appel à l’axiome du choix, qu’il existe des homomorphismes u autres que les homothéties.

Revenons aux équations fonctionnelles vérifiées par f et g . En intégrant ces équations, on voit que f et g sont, en fait, de classe C¹. On peut donc dériver des équations par rapport à y ; ce qui donne:

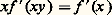et donc, pour y = 1,

de même, on a: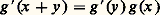

et donc, pour y = 0,

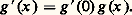En particulier, on voit que f (x ) = k /x , ce qui conduit à étudier les primitives de x 料 1/x . C’est ainsi que l’on définira le logarithme au chapitre 2. La fonction exponentielle s’en déduit alors par passage à la fonction réciproque (chap. 3). Nous aurons besoin pour cela du théorème classique d’inversion.

Inversion des fonctions monotones

Dans ce qui suit, nous nous limiterons, pour des facilités d’énoncé, à des fonctions croissantes, étant entendu que les résultats correspondants pour les fonctions décroissantes s’en déduisent immédiatement.

Soit f une fonction à valeurs réelles définie et strictement croissante dans un intervalle I = (a , b ); I est quelconque, borné ou pas (ce qui veut dire qu’on peut avoir a = 漣 秊 par exemple), ouvert, fermé ou semi-ouvert. Par des arguments très analogues à ceux qui sont exposés à la fin du chapitre 4 de l’article CALCUL INFINITÉSIMAL - CALCUL À UNE VARIAble, on peut montrer que f (x ) tend vers une limite 見 (resp. 廓 ), éventuellement égale à 漣 秊 (resp. + 秊), pour x tendant vers a par valeurs supérieures (resp. vers b par valeurs inférieures): cette limite en a est la borne inférieure (ou 漣 秊, si cet ensemble n’est pas borné inférieurement) de l’ensemble des nombres f (x ), x 捻 I.

Si f est de plus continue, on déduit facilement du théorème 14 bis du même article (chap. 9), dit théorème des valeurs intermédiaires, que f réalise une bijection de I sur l’intervalle J = ( 見 , 廓 ), les extrémités correspondantes de I et J étant de même nature, incluses ou exclues simultanément. De plus, la bijection réciproque de J sur I est, sous ces hypothèses, continue. Ainsi, on peut énoncer le résultat suivant: si f est une application continue strictement croissante d’un intervalle I dans R, alors c’est une bijection de I sur l’intervalle image et la bijection réciproque est continue. Si f est dérivable, l’application réciproque est dérivable en tout point x = f (y ) 捻 J tel que f (y ) 0 et on a:

On verra dans ce qui suit de nombreux exemples de cette situation.

2. Logarithmes

Définition

Il n’existe pas de fonction rationnelle admettant pour dérivée 1/x ; pourtant, cette fonction est définie et continue pour x 礪 0, et, par suite (cf. CALCUL INFINITÉSIMAL – Calcul à une variable, chap. 5), elle admet des primitives dans cet intervalle. Ces primitives constituent donc de «nouvelles» fonctions dont nous allons étudier les propriétés. Elles diffèrent toutes entre elles d’une constante, et il suffit d’en examiner une.

On appelle logarithme népérien ou naturel la primitive de 1/x dans ]0, 秊[ qui s’annule pour x = 1, soit:

ainsi, c’est une fonction dérivable, de dérivée 1/x . Géométriquement, si x 礪 1, c’est la mesure de l’aire comprise entre l’hyperbole d’équation Y = 1/X et les deux droites X = 1 et X = x (fig. 1); on a donc ln x 麗 0 pour 0 麗 x 麗 1 et ln x 礪 0 pour x 礪 1. On utilisera dans l’ouvrage la notation normalisée anglo-saxonne ln x .

Établissons dès maintenant la propriété fondamentale du logarithme népérien: c’est un homomorphisme (en fait, comme on le verra ci-dessous, un isomorphisme ) du groupe multiplicatif R⁺ dans le groupe additif R. Soit y un nombre réel positif; la fonction f (x ) = ln xy a la même dérivée que la fonction ln x :

et, par suite, ces deux fonctions diffèrent d’une constante, soit:

faisant x = 1, on a k = ln y , d’où la relation fonctionnelle:

On en déduit immédiatement, pour tout entier n 捻 Z,

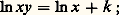
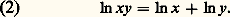
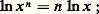plus généralement, avec la convention des exposants fractionnaires; si 見 = p/q , q 礪 0, rappelons que, par définition, x 見 = q 連x ^p ; on a donc: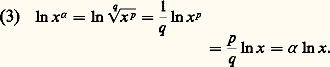

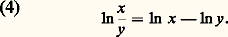D’autre part, si x et y sont des nombres positifs quelconques, on a y (x/y ) = x , d’où:

Comportement et graphe

La fonction logarithme népérien est strictement croissante pour x 礪 0, car sa dérivée est strictement positive dans cet intervalle.

Étudions le comportement du logarithme lorsque x tend vers l’infini. Pour tout entier n , on a:

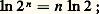si A est un nombre positif, soit N un entier plus grand que A /(ln 2). Pour x 礪 2^N = B, on a:

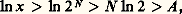ce qui montre que:

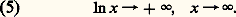On en déduit facilement le comportement de ln x pour x tendant vers 0 par valeurs positives; si A est un réel positif, on a, pour le même choix de N que ci-dessus,

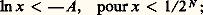ainsi:

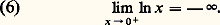Précisons le comportement de ln x en montrant que cette quantité est asymptotiquement négligeable devant x pour x tendant vers l’infini. En effet, pour t 閭 1, on a par exemple:

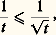d’où, pour x 閭 1,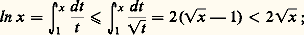

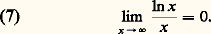ainsi: ln x /x 麗 2/ 連x , ce qui entraîne bien:

Toutes ces propriétés permettent de tracer le graphe de L (fig. 2). On peut préciser le tracé en remarquant que la fonction est concave , car sa dérivée seconde 漣1/x ² est négative; la tangente au point d’abcisse 1 est de pente égale à 1, ce qui équivaut à:

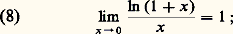on exprime cela en disant que ln (1 + x ) est équivalent à x pour x tendant vers 0 (cf. calculs ASYMPTOTIQUES). On peut préciser le comportement de ln (1 + x ) au voisinage de x = 0 par le développement en série:

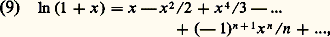valable pour |x | 麗 1, qui s’obtient en intégrant terme à terme la série géométrique:

dont la somme est égale à la dérivée 1/(1 + x ) de ln (1 + x ).

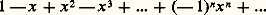C’est à partir de cette série que l’on peut calculer les valeurs numériques des logarithmes (cf. CALCUL NUMÉRIQUE - Histoire). En définitive, le logarithme népérien L: R⁺R est continu, strictement croissant et tend vers 漣 秊 et + 秊 pour x tendant vers 0 (par valeurs supérieures) et vers + 秊 respectivement; d’après le théorème d’inversion (cf. chap. 1) c’est donc une bijection, c’est-à-dire un isomorphisme (continu) du groupe multiplicatif des nombres réels positifs sur le groupe additif de tous les nombres réels. La bijection réciproque est un isomorphisme du groupe R sur le groupe R⁺: c’est la fonction exponentielle que nous examinerons dans le chapitre suivant. En particulier, il existe un unique nombre réel positif dont le logarithme népérien est égal à 1; c’est le célèbre nombre e , dont la transcendance a été établie par C. Hermite en 1873.

Autres logarithmes

Proposons-nous maintenant de caractériser tous les homomorphismes continus du groupe multiplicatif R⁺ dans le groupe additif R. Soit f l’un d’entre eux; tout nombre réel u s’écrit de manière unique:

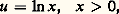avec x = L ^-1(u ); l’application 﨏 : RR, qui, à u 捻 R, fait correspondre f (x ) = f (L ^-1(u )), en accord avec le diagramme suivant:

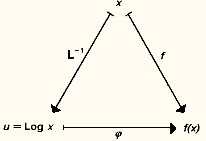est un homomorphisme continu du groupe additif R dans lui-même et est donc (cf. chap. 1) de la forme 﨏 (u ) = ku , où u est une constante. Ainsi f (x ) = k ln x , c’est-à-dire que f est un multiple scalaire du logarithme népérien.

Soit f = k L un tel logarithme; il existe un unique nombre a 礪 0, défini par ln a = 1/k , tel que f (a ) = 1. On dit que c’est la base de la fonction logarithme f et on note:

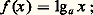avec cette définition, le logarithme népérien est de base e . On a des formules de changement de base du type:

Pour les calculs pratiques, on utilise des tables de logarithmes décimaux, de base a = 10; le passage d’un système à l’autre s’effectue au moyen des formules:

Historique

L’idée qui est historiquement à la base de la notion de logarithme est la comparaison de la suite des entiers et de la suite des puissances correspondantes d’un nombre a :

déjà étudiée par Archimède dans son traité de l’Arénaire ; dans le Triparty en la science des nombres (1484) Nicolas Chuquet remarqua que, si on fait correspondre les termes de même rang, à la somme de deux nombres de la progression arithmétique correspond le produit des nombres de la progression géométrique. Cette correspondance fut étendue aux exposants négatifs et fractionnaires par Michael Stifel (1544), mais la notion de logarithme ne se développa vraiment qu’au début du XVII^e siècle, lorsque l’Écossais John Napier, ou Neper (Mirifici logarithmorum canonis descriptio , Édimbourg, 1614), puis le Suisse Joost Bürgi (Aritmetische und geometrische Progresstabulen , Prague, 1620) eurent l’idée d’introduire des nombres intercalaires en quantité suffisante et construisirent des tables permettant de passer d’une progression à l’autre. Neper a rendu «continue» la correspondance entre les deux progressions en utilisant une image cinématique; il les supposa engendrées l’une et l’autre par mouvement continu («par fluxion»): deux points mobiles se déplacent le long d’une droite à partir d’une même position initiale, l’un M avec une vitesse uniforme, l’autre N avec une vitesse proportionnelle à son abscisse; le logarithme de l’abscisse de N est alors par définition l’abscisse de M.

Les premières tables de logarithmes décimaux sont dues à Henry Briggs (Arithmetica logarithmica , 1624) qui fait des logarithmes un moyen de calcul numérique pratique. Les fonctions logarithme et exponentielle s’introduisent en analyse au cours du XVII^e siècle et sont intimement liées à la création et au développement du calcul infinitésimal (cf. CALCUL INFINITÉSIMAL - Histoire).

3. Exponentielles réelles

On va maintenant définir la fonction exponentielle comme fonction réciproque du logarithme népérien.

La fonction exponentielle

On appelle fonction exponentielle l’isomorphisme E : RR⁺, réciproque du logarithme népérien; ainsi, pour tout nombre réel x , E(x ) = exp x est l’unique nombre réel 礪 0 dont le logarithme népérien est égal à x , soit:

cela entraîne aussi, par composition de L et E que, pour tout x 捻 R et pour tout y 捻 R⁺, on a:

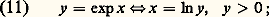
Puisque la fonction logarithme népérien est strictement croissante et dérivable de dérivée toujours non nulle, il en est de même de la fonction exponentielle; son graphe est le symétrique du graphe de L par rapport à la première bissectrice d’équation y = x (fig. 3).

La dérivée en x de la fonction exponentielle est l’inverse de la dérivée de la fonction logarithme népérien au point y = exp x soit: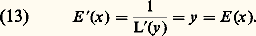

Plus précisément, la fonction exponentielle est l’unique solution sur R du problème de Cauchy:

ainsi la fonction exponentielle est indéfiniment dérivable et égale à toutes ses dérivées. La formule de Taylor en 0 s’écrit ici (cf. formule 47, CALCUL INFINITÉSIMAL Calcul à une variable):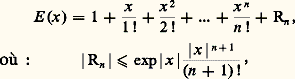

qui, pour tout x , tend vers 0 lorsque n tend vers l’infini. En effet, pour tout x , la suite u ^p = x ^p /p ! vérifie u ^{p +1}/u ^p = x /(p + 1), qui est inférieur à 1/2 en valeur absolue pour p assez grand, disons p 閭 P ; pour p 閭 P , on a donc |u ^{p +1}| 諒 (1/2)^p-P , ce qui montre que la suite u ^p tend vers 0 pour p tendant vers + 秊. Ainsi, E(x ) est, pour tout x 捻 R, la somme de sa série de Taylor, soit:

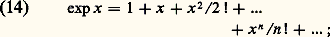Pour x+ 秊, on déduit facilement de (7) le comportement asymptotique:

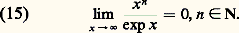Soit enfin une dernière propriété de la fonction exponentielle. Pour tout entier n :

puisque:

cela conduit à la formule: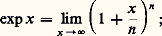

ce type de raisonnement (dû en subtance à Euler) demande, bien entendu, à être établi rigoureusement, par exemple par les développements limités.

Le nombre e

Pour x = 1, E (1) = e , base des logarithmes népériens. Ce nombre est la somme de la série:

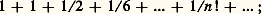c’est aussi la limite de l’expression:

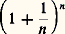pour n tendant vers l’infini.

Une valeur approchée de e , à 10^-24 près, est:

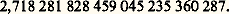Si n est un entier relatif, on a E (n ) = e ⁿ , puisque ln e ⁿ = n ln e = n . Plus généralement, si x = p /q , q 礪 0, est un nombre rationnel, on a:

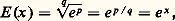avec la convention des exposants fractionnaires (cf. nombres RÉELS). Ainsi, la fonction exponentielle est un prolongement continu à R tout entier de l’application x 料 e ^x de Q dans R⁺ définie par la convention des exposants fractionnaires; cela conduit à généraliser cette notation en posant par définition :

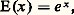pour tout réel x ; le fait que l’exponentielle est un homomorphisme de groupe s’écrit maintenant:

formule valable pour x et y réels quelconques.

Trigonométrie hyperbolique

Introduisons maintenant les fonctions hyperboliques, qui jouent pour la géométrie du plan hyperbolique le même rôle que les fonctions circulaires pour le plan euclidien (cf. GROUPES - Groupes classiques et géométrie, chap. 3).

Pour tout nombre réel x , on appelle cosinus hyperbolique de x , sinus hyperbolique de x et tangente hyperbolique de x respectivement les nombres: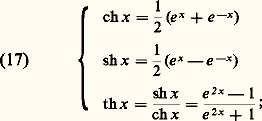

remarquons que le cosinus hyperbolique est une fonction paire, tandis que les deux autres sont des fonctions impaires.

Un calcul simple montre que l’on a:

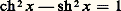pour tout x ; si a et b sont deux nombres réels la propriété (16) de la fonction exponentielle entraîne les formules d’addition suivantes:

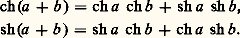Par dérivation dans (17), on obtient facilement:

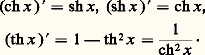Puisque ch x 閭 1, il en résulte que sh x est une application strictement croissante de R dans R et on voit que sh x tend vers 漣 秊 et + 秊 pour x tendant vers 漣 秊 et + 秊 respectivement: cette fonction réalise donc une bijection de R sur R. Puisque sh 0=0, le nombre sh x est du signe de x ; par suite la fonction paire ch x est strictement décroissante pour x 諒 0 et strictement croissante pour x 閭 0; d’autre part, ch x tend vers + 秊, pour x tendant vers + 秊 ou vers 漣 秊. Enfin, la fonction th x , dont la dérivée est toujours 礪 0, est strictement croissante; pour x tendant vers l’infini, on a:

et, par suite, th x réalise une bijection de R sur l’intervalle ] 漣 1, + 1[.

On a représenté les graphes des fonctions hyperboliques sur la figure 4.

L’application t 料 (ch t , sh t ) est une représentation paramétrique de la branche d’hyperbole x ² 漣 y ² = 1, x 礪 0, d’où le nom de trigonométrie hyperbolique , par analogie à la trigonométrie «circulaire». La bijection réciproque s’appelle amplitude et se note u 料 Am u .

On désigne par Arg sh x la bijection de R sur R réciproque de sh x , par Arg ch x la bijection de ]1, 秊[ sur R⁺ réciproque de la restriction de ch x à R⁺ et enfin par Arg th x la bijection de [ 漣 1, + 1[ sur R réciproque de th x . Ainsi:

On obtient e ^2y 漣 2xe ^y 漣 1 = 0, en remplaçant sh y par son expression exponentielle dans x = sh y ; d’où e ^y = x + 連x ² + 1, puisque e ^y 礪 0. Ainsi, Arg sh x s’exprime au moyen du logarithme népérien par la formule: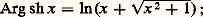

par des raisonnements analogues, on aurait:

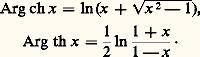Les dérivées des fonctions hyperboliques inverses sont très simples et se calculent en appliquant le théorème du chapitre 1 sur la dérivée d’une fonction réciproque; nous ne détaillerons pas le calcul, nous contentant d’indiquer le résultat:

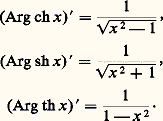Pour terminer ces quelques lignes sur la trigonométrie hyperbolique, donnons enfin les développements en série de ch x , sh x , qui se déduisent immédiatement de (14) et de (17), et de Arg th x , qui s’obtient par intégration à partir de la série géométrique:

avec |x | 麗 1:

Fonction exponentielle de base a

Soit a un nombre réel strictement positif. Pour x rationnel, on a lna ^x = x ln a (avec la convention des exposants fractionnaires; cf. supra. chap. 1); d’où d’après (12),

Désirant étendre cette notation, nous prendrons l’expression (18) comme définition de a ^x pour tout x réel; la fonction E ^a définie par E ^a (x ) = a ^x s’appelle la fonction exponentielle de base a .

Pour a = 1, on a 1^x = 1 pour tout nombre réel x . Pour a 礪 0, a 1, faisons le lien avec le logarithme de base a ; le logarithme de base a réalise un isomorphisme (strictement croissant si a 礪 1, strictement décroissant si a 麗 1) du groupe multiplicatif R⁺ sur le groupe additif R; l’isomorphisme réciproque fait correspondre à tout réel x l’unique nombre y 礪 0 tel que: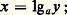

puisque:

d’où ln y = x ln a ; on en déduit:

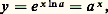ce qui montre que la fonction exponentielle de base a est la fonction réciproque du logarithme de base a . C’est donc un isomorphisme de groupes, d’où:

Les fonctions x 料 a ^x sont les seuls homomorphismes continus du groupe additif R dans le groupe multiplicatif R⁺.

De la définition (18) résulte aussi: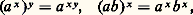

pour a , b réels positifs et x , y réels quelconques. En effet, pour la première de ces formules par exemple, on a:

La fonction exponentielle de base a est strictement croissante pour a 礪 1; elle est strictement décroissante pour a 麗 1; sa dérivée s’obtient facilement sous la forme (18); on a: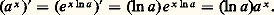

Fonctions puissances

Soit u un nombre réel quelconque; on appelle fonction puissance l’application P ^u de R⁺ dans R⁺ qui, à x 礪 0, fait correspondre le nombre réel positif x ^u . Par définition, on a donc: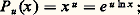

de (19) résulte que l’on a, pour x 礪 0, y 礪 0,

c’est-à-dire que P ^u est un homomorphisme du groupe multiplicatif R⁺ dans lui-même; il résulte de ce qui précède que c’est un isomorphisme pour u 0, l’isomorphisme réciproque étant P ^u size=1^漣1 = P ^1/u . Pour u 閭 0, P ^u est strictement croissant et se prolonge par continuité pour x = 0 en posant P ^u (x ) = 0; pour u 麗 0, P ^u est strictement décroissant. Les fonctions x 料 x ^u sont les seuls homomorphismes continus de R⁺ dans R⁺. Dans tous les cas, on a, pour x 麗 0,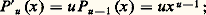

sur la figure 5, on a représenté les graphes des fonctions puissances pour diverses valeurs de u .

Indiquons que l’on peut montrer, par des majorations explicites que nous ne ferons pas ici, que le reste de la formule de Taylor de P ^u au voisinage de 1 tend vers 0, pour x assez voisin de 1; on obtient ainsi le développement en série:

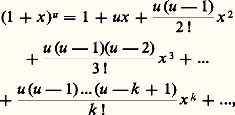valable pour |x | 麗 1, qui généralise au cas d’un exposant réel quelconque la classique formule du binôme de Newton.

Enfin, décrivons le comportement asymptotique des fonctions puissances pour u 礪 0, la fonction P ^u tend vers l’infini «plus vite» que la fonction logarithme et «moins vite» que la fonction exponentielle, lorsque x tend vers l’infini, soit:

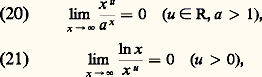comme cela résulte facilement de (15).

4. Extension du domaine complexe et trigonométrie

Nous commencerons par le cas de la fonction exponentielle, le plus simple car le développement en série entière (14) converge encore pour tout x complexe , et cela suggère d’étendre cette fonction au domaine complexe en la définissant , dans ce cas, comme somme de la série correspondante.

L’exponentielle complexe

La série:

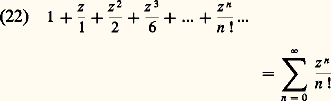est absolument convergente pour tout nombre complexe z . Pour z réel, la somme est e ^z . Pour z 捻 C, nous noterons encore exp z ou e ^z la somme de cette série. D’après la règle de multiplication des séries absolument convergentes, on a, pour a , b 捻 C,

ainsi, on a l’importante formule d’addition: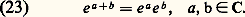

Puisque 1 = e ⁰ = e ^z e size=1^{漣 z} pour tout z 捻 C, on a toujours e ^z 0 et, ainsi, la formule d’addition exprime que l’exponentielle complexe définit un homomorphisme du groupe additif C de tous les nombres complexes dans le groupe multiplicatif C des nombres complexes non nuls.

En outre, pour tout a 捻 C, on a:

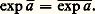Enfin, par dérivation terme à terme de la série correspondante, on voit que, pour tout nombre complexe a , la fonction de variable réelle

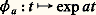satisfait à la relation 﨏 ^a (t ) = a 﨏 ^a (t ). Plus précisément 﨏 ^a est l’unique solution sur R du problème de Cauchy: y = ay , y (0) = 1.

Fonctions circulaires

Soit z = x + iy un nombre complexe, on a:

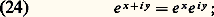la fonction exponentielle e 料 e ^x ayant été étudiée, nous allons examiner maintenant la fonction y 料 e ^iy .

Pour t réel, on appelle respectivement cosinus et sinus de t les parties réelle et imaginaire de e ^it , soit, par définition,

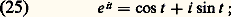il en résulte immédiatement les «formules d’Euler »:

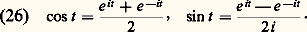D’après ce qui précède, l’application 﨏 : t 料 exp it est un homomorphisme du groupe additif R dans le groupe multiplicatif U des nombres complexes de module 1 (cf. nombres COMPLEXES) et 﨏 (t ) = i 﨏 (t ). L’étude de ce morphisme constitue ce qu’on appelle traditionnellement la trigonométrie (fig. 6).

La relation |e ^it | = 1 signifie que:

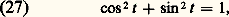qui est la relation fondamentale de la trigonométrie.

Par ailleurs, la propriété fonctionnelle:

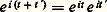donne, en séparant parties réelle et imaginaire, les formules d’addition de la trigonométrie:

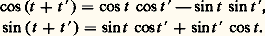Remplaçant e ^it et e size=1^{漣 it} dans les formules d’Euler par leurs développements en série déduits de (22), on obtient les développements en séries entières, valables pour tout nombre réel t , des fonctions trigonométriques:

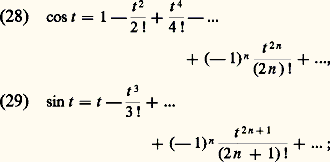ainsi les fonctions sinus et cosinus sont indéfiniment dérivables. Par dérivation des formules d’Euler, ou des développements en série qui précèdent, on a:

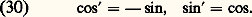Le nombre size=5神

Pour t = 2, on a:

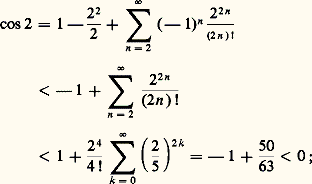puisque la fonction cosinus est continue et égale à 1 pour t = 0, il existe un plus petit nombre réel 精 礪 0 tel que cos 精 = 0. Nous désignerons par la lettre grecque 神 , notation traditionnelle depuis Euler, le nombre 神 = 2 精 . Ce nombre 神 , dont la transcendance a été établie par F. Lindemann en 1882, est égal à la moitié de la longueur du cercle de rayon 1 ^{[cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE]}. Une valeur approchée à 10 size=1^漣20 près (cf. ALGORITHMIQUE, CALCUL NUMÉRIQUE - Histoire) est:

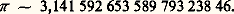Ainsi, par définition de 神 , on a cos t 礪 0 dans l’intervalle ]0, 神 /2[, ce qui entraîne, d’après (30), que la fonction sinus est strictement croissante dans l’intervalle [0, 神 /2]. Puisque sin 0 = 0, cette fonction est donc strictement positive dans l’intervalle ]0, 神 /2], ce qui entraîne toujours d’après (30), que le cosinus est strictement décroissant dans cet intervalle. On peut alors constituer, entre 0 et 神 /2, le tableau de variation des fonctions circulaires.

Pour t = 神 /2, la relation (27) entraîne que le sinus est, en valeur absolue, égal à 1; par suite puisque ce nombre est positif sin 神 /2 = 1. Ainsi:

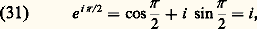d’où, en utilisant la formule d’addition,

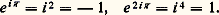Pour tout nombre complexe z , on a donc:

ce qui montre que la fonction exponentielle complexe est périodique, de période imaginaire pure 2 i 神 ; en particulier, les fonctions circulaires sont périodiques de période 2 神 et il suffit de les étudier dans l’intervalle [0,2 神 ] par exemple. Leur variation dans cet intervalle se déduit immédiatement de leur variation dans [0, 神 /2] en utilisant les relations: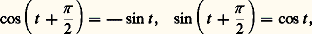

qui ne font qu’exprimer que:

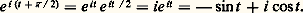On peut ainsi former le tableau de variation de ces fonctions et construire leurs graphes (fig. 7).

On introduit aussi la fonction tangente , définie pour t = (2k + 1) 神 /2, k 捻 Z par:

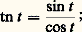elle est périodique de période 神 , de dérivée 1/cos² t = 1 + tn² t 礪 0, donc strictement croissante dans l’intervalle ouvert ] 漣 神 /2, 神 /2[ (fig. 8).

Le tableau de variation ci-dessus montre que, pour tout couple de nombres réels u , v tels que u ² + v ² = 1, il existe un nombre réel, et un seul, t dans l’intervalle ] 漣 神 , 神 ] tel que:

Par suite, l’application t 料 e ^it est un homomorphisme surjectif de R sur U dont le noyau est le sous-groupe 2 神 Z constitué des multiples entiers de 2 神 ; autrement dit, deux nombres réels ont les mêmes cosinus et sinus si et seulement s’ils diffèrent d’un multiple entier de 2 神 .

Fonctions circulaires réciproques

Les fonctions circulaires n’étant pas monotones dans R tout entier, il ne sera possible de définir des fonctions réciproques que si l’on se restreint à des intervalles sur lesquels ces fonctions sont strictement monotones. On définit ainsi les fonctions Arc sinus, Arc cosinus et Arc tangente comme fonctions réciproques de la restriction du sinus à [ 漣 神 /2, 神 /2], de la restriction du cosinus à [0, 神 ] et enfin de la restriction de la tangente à ] 漣 神 /2, 神 /2[ respectivement. Ainsi, Arc sin est une bijection strictement croissante de [ 漣 1, + 1] sur [ 漣 神 /2, 神 /2] et:

Arc cos est une bijection strictement décroissante de [ 漣 1, + 1] sur [0, 神 ] et:

Arc tn est une bijection strictement croissante de R sur ] 漣 神 /2, + 神 /2[ (cf. fig. 8) et :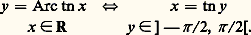

Le théorème des fonctions réciproques permet de calculer les dérivées de ces fonctions. On a:

Ces fonctions sont d’usage constant en calcul intégral et permettent d’écrire le nombre 神 comme une intégrale définie, par exemple: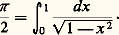

Trigonométrie complexe

Les fonctions hyperboliques et les fonctions circulaires s’étendent au domaine complexe de manière naturelle, soit en utilisant des développements en série, soit (ce qui revient au même, puisque e ^z est défini comme somme d’une série) au moyen des formules:

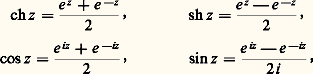qui mettent en évidence, par passage au domaine complexe, les liens étroits qui existent entre la trigonométrie hyperbolique et la trigonométrie circulaire. Ces fonctions sont analytiques dans tout le plan, et on a des relations du type:

valables en particulier pour z réel, qui permettent de déduire la trigonométrie hyperbolique de la trigonométrie circulaire et vice versa.

Fonction argument principal

On a vu que t 料 e ^it est une bijection de ] 漣 神 , 神 ] sur U, et ainsi t 料 (cos t , sin t ) est une représentation paramétrique du cercle trigonométrique: mais la bijection réciproque n’est pas continue au point 漣 1. En revanche, l’application 﨏 : t 料 e ^it est un homéomorphisme de ] 漣 神 , 神 [ sur U 漣漣 1, la bijection réciproque 祥 étant définie par: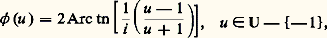

le nombre (1/i )((u 漣 1)/(u + 1)) étant réel. En effet, pour tout nombre réel t de l’intervalle ] 漣 神 , 神 [, on a:

Tout nombre complexe z 0 peut s’écrire de manière unique sous la forme: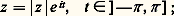

rappelons que t s’appelle l’argument principal , noté Arg z , du nombre complexe z 0. D’après ce qui précède, l’application:

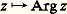est continue sur C 漣 R^-, complémentaire dans C de l’ensemble des nombres réels négatifs, aussi appelé plan fendu; on appelle cette application fonction argument principal .

En outre, si x ⁰ est un nombre réel strictement négatif, on a:

ce qui montre que la fonction argument principal ne se prolonge pas en une fonction continue sur C 漣0.

Mentionnons enfin l’important théorème suivant:

Théorème de relèvement . Soit f une application de classe C^p , p 閭 0, d’un intervalle I de R et à valeurs dans U. Alors, il existe une application 﨏 , de classe C^p , de I dans R telle que, pour tout t ,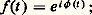

En outre, deux fonctions continues satisfaisant à cette relation diffèrent d’une constante de la forme 2k 神 , k 捻 Z.

Logarithmes complexes

Les tentatives pour étendre les logarithmes aux nombres négatifs, puis aux nombres complexes, sont à l’origine d’une controverse célèbre qui a opposé, pendant près d’un demi-siècle, les plus grands esprits mathématiques du XVIII^e siècle. Jean Bernoulli admettait implicitement l’existence des logarithmes des nombres complexes, par analogie avec le cas réel, et il les introduisait tout naturellement à propos de l’intégration des fractions rationnelles, comme primitives d’éléments simples de la forme 1/(z 漣 a ), a 捻 C. Bernoulli soutenait que:

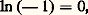car son double ln 1 = ln (face=F0019 漣 1)² est nul; il en résultait que ln x = ln (face=F0019 漣 x ) pour tout réel positif, puis que ln (face=F0019 漣 1) = 0 puisque (face=F0019 漣 1)² = 漣 1. Mais ces résultats étaient en contradiction avec d’autres formules obtenues par J. Bernoulli lui-même.

Leibniz, pour sa part, soutenait que les logarithmes des nombres négatifs ne peuvent être réels. Une mémorable correspondance s’ensuivit entre les deux mathématiciens, de 1700 à 1716.

Dès 1728, L. Euler eut le pressentiment qu’il fallait abandonner l’unicité de la détermination si on voulait développer une théorie non contradictoire des logarithmes des nombres imaginaires. Dans un remarquable mémoire de 1749, il expose une théorie complète, en montrant que tout nombre non nul a une infinité de logarithmes possibles. Pourtant cela ne convainquit pas d’Alembert, qui continua la polémique.

Par analogie avec le cas réel, on est donc conduit à se demander si on peut définir le «logarithme» d’un nombre complexe 﨣 0, c’est-à-dire à chercher un nombre complexe z tel que e ^z = 﨣 . Remarquons tout de suite que, s’il existe un tel nombre complexe z ⁰, alors la périodicité de la fonction exponentielle dans le domaine complexe, formule (32), entraîne que tout nombre complexe de la forme:

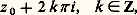est aussi un «logarithme» de 﨣 . Ainsi, si on veut avoir une théorie des logarithmes dans le domaine complexe, il sera indispensable d’associer à tout nombre une infinité de logarithmes.

Pour étudier la fonction exponentielle, nous nous limiterons d’abord, vu sa périodicité, à une «bande» du plan complexe dans laquelle la partie imaginaire de z varie dans un intervalle semi ouvert de longueur 2 神 ; nous prendrons ici la bande B formée des nombres complexes z = x + iy tels que 漣 神 麗 y 諒 + 神 .

La relation:

équivaut aux relations:

L’unique solution dans B de l’équation e ^z = 﨣 s’appelle logarithme principal de 﨣 et se note ln 﨣 . Ainsi, par définition, pour 﨣 捻 C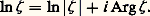

Toutes les autres solutions de l’équation e ^z = 﨣 sont alors de la forme:

la formule d’addition ne s’applique pas toujours à la détermination principale du logarithme mais peut s’énoncer ici: si lg 﨣 et lg 﨣 sont des logarithmes de 﨣 et 﨣 respectivement, alors lg 﨣 + lg 﨣 est un logarithme de 﨣 﨣 .

La fonction 﨣 料 ln 﨣 est continue sur le plan fendu C 漣 R^-; on l’appelle détermination principale du logarithme . C’est une fonction analytique (cf. FONCTIONS ANALYTIQUES - Fonctions d’une variable, chap. 4).

5. Développements eulériens des fonctions transcendantes élémentaires

Dans son Introductio in analysin infinitorum (1748), L. Euler définit l’exponentielle complexe par la formule:

par suite, il considère la fonction exponentielle et les fonctions trigonométriques qui s’en déduisent comme des «polynômes de degré infini».

En particulier:

écrivant le polynôme du second membre comme un produit de facteurs du second degré et faisant tendre n vers l’infini, il obtient la relation:

qui est le développement de sin z en produit infini (produit eulérien).

Cette formule, valable pour tout z 捻 C, met en évidence les zéros de la fonction sinus, tout comme la décomposition d’un polynôme comme produit de facteurs du premier degré (théorème de d’Alembert-Gauss, cf. nombres COMPLEXES, chap. 2).

Par des procédés analogues, il obtient les développements:

valables pour z k 神 , k 捻 Z.

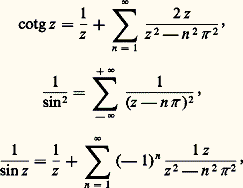Cette fois, les fonctions de gauche dans les formules apparaissent comme des «fractions rationnelles de degré infini»; au second membre figure alors la somme des parties principales, en chacun de leurs pôles, de ces fonctions (généralisation de la décomposition d’une fraction rationnelle en éléments simples).

La théorie des fonctions analytiques fournit un cadre théorique permettant de généraliser de telles formules (décompositions de Weierstrass et de Mittag-Leffler; cf. FONCTIONS ANALYTIQUES - Fonctions d’une variable, chap. 8).

Encyclopédie Universelle. 2012.